A group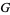 
is a finite or infinite set of elements together with a binary operation (called the group operation) that together satisfy the four fundamental properties of closure, associativity, the identity property, and the inverse property. The operation with respect to which a group is defined is often called the "group operation," and a set is said to be a group "under" this operation. Elements 
, 
, 
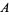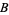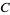, ... with binary operation between 
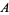and 
denoted 
form a group if
is a finite or infinite set of elements together with a binary operation (called the group operation) that together satisfy the four fundamental properties of closure, associativity, the identity property, and the inverse property. The operation with respect to which a group is defined is often called the "group operation," and a set is said to be a group "under" this operation. Elements , , , ... with binary operation between and 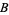denoted 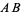form a group if
1. Closure: If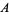 
and 
are 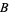two elements in 
, then the product 
is also in 
.
and are two elements in 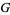, then the product 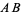is also in .
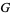2. Associativity: The defined multiplication is associative, i.e., for all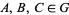 
, 
.
, .
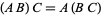(a.k.a. 1, 
, or 
) such that 
for every element 
.
4. Inverse: There must be an inverse (a.k.a. reciprocal) of each element. Therefore, for each element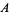 
of 
, the set contains an element 
such that 
.
of 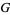, the set contains an element 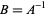such that .
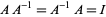A group is a monoid each of whose elements is invertible.
A group must contain at least one element, with the unique (up to isomorphism) single-element group known as the trivial group.
The study of groups is known as group theory. If there are a finite number of elements, the group is called a finite group and the number of elements is called thegroup order of the group. A subset of a group that is closed under the group operation and the inverse operation is called a subgroup. Subgroups are also groups, and many commonly encountered groups are in fact special subgroups of some more general larger group.
A basic example of a finite group is the symmetric group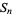 
, which is the group of permutations (or "under permutation") of 
objects. The simplest infinite group is the set of integers under usual addition. For continuous groups, one can consider the real numbers or the set of 
invertible matrices. These last two are examples of Lie groups.
, which is the group of permutations (or "under permutation") of 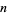objects. The simplest infinite group is the set of integers under usual addition. For continuous groups, one can consider the real numbers or the set of 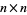invertible matrices. These last two are examples of Lie groups.http://mathworld.wolfram.com/Group.html
No comments:
Post a Comment
Note: Only a member of this blog may post a comment.