The fundamental theorems and propositions on Group Theory from
www.ibmaths4u.com
1.

is a group under addition modulo n. With identity 0 and the inverse of
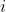
is the

2. The number of elements of a group is its order
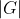
3. The order of an element g, which is denoted by

, in a group G is the smallest positive integer n such that
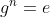
4. Cyclic group
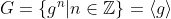
and g is called a generator of
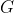
5. The order of the generator is the same as the order of the group it generated.
6. Let G be a group, and let x be any element of G. Then,
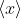
is a subgroup of G.
7. Let
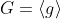
be a cyclic group of order n.
Then
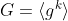
if and only if gcd(n,k)=1.
8. Every subgroup of a cyclic group is cyclic.
9. Every cyclic group is Abelian.
10. If G is isomorphic to H then G is Abelian if and only if H is Abelian.
11. If G is isomorphic to H then G is Cyclic if and only if H is Cyclic.
12. Lagrange’s Theorem: If G is a finite group and H is a subgroup of G, then the order of H divides G.
13. In a finite group, the order of each element of the group divides the prder of the group.
14. A Group of prime order is cyclic.
15. For any

where e is the identity element of the group G.
16. An infinite cyclic group is isomorphic to the additive group
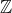
17. A cyclic group of order n is isomorphic to the additive group
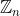
of integers modulo n.
18. Let p be a prime. Up to isomorphism, there is exactly one group of order p.
19. Let (G, *) be a group and
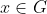
. If
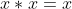
, then
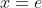
, where

is the identity element of the group G.
20. In a Cayley table for a group (G, *), each element appears exactly once in each row and exactly once in each column.
21. A group (G,*) is called a finite group if G has only a finite number of elements. The order of the group is the number of its elements.
22. A group with an infinite number of elements is called an infinite group.
23. If (G,*) is a group, then ({e},*) and (G,*) are subgroups of (G,*) and are called trivial.
24. Let G be a group and H be a non-empty subset of G. then H is a subgroup of G if and only if for all

.
25. Let G be a group and H be a finite non-empty subset of G. then H is a subgroup of G if and only if for all

.
26. Let
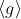
be a finite group of order n.
Then

27. Let
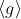
be a finite cyclic group. Then the order of g equals the order of the group.
28. A finite group G is a cyclic group if and only if there exists an element
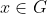
such that the order of this element equals the order of the group (
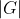
).
29. Let G be a finite cyclic group of order n. Then froe every positive divisor d of n, there exists a unique subgroup of G of order d.
30. Let G be a group of finite order n. Then the order of any element x of G divides n and
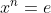
31.Let G be a group of prime order. Then g is cyclic.
)
=0.3)
 to that of
to that of ) , using the transformation
, using the transformation 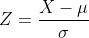
=0.3%20\Rightarrow%20P(\frac{X-%20\mu}{\sigma}%20\geq%20\frac{53-%20\mu}{2})=0.3)
=0.3)
 :1
:1 :0
:0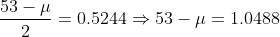
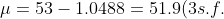)